Uno de los problemas que, desde tiempo inmemorial, ha interesado a los filósofos es el del infinito. Borges ha tratado en sus cuentos este tema. “El libro de arena” es uno de los últimos cuentos de Borges. Trata de un libro que tiene un número de páginas infinito. Cuando uno abre una página en que aparece la ilustración de un ancla y cierra el libro, las probabilidades de volver a encontrar la página que vio anteriormente son computables en cero. Los números de páginas en el libro están desordenados. Por ejemplo, una página es la 999 y la siguiente es la 40.000. En este libro es necesario que la numeración sea así. ¿Por qué? Porque es imposible llegar a la primera página. También es imposible llegar a la última. Con los números pasa igual. Los números racionales forman un conjunto denso, lo que quiere decir que entre dos racionales siempre se puede encontrar otro racional. Un ejemplo parecido al del libro en el que no se puede encontrar el final lo tenemos en el conjunto de los racionales menores que 2. ¿Cuál es el mayor número de este conjunto? No es el 2, porque el 2 está fuera del conjunto. ¿Será el 1,99? No, porque el 1,999 es mayor que el 1,99. Y el 1,9999 mayor que 1,999. Y así sucesivamente. Conclusión: no existe un número mayor, un máximo de ese conjunto. (No digan que lo es un número con un número infinito de 9s, porque este número, en realidad, es igual a 2). Igual sucede con el libro. Entre un determinado lugar del libro (cualquiera que éste sea) y el final siempre existen infinitas páginas.
El cuento de Borges nos recuerda una de las ramas más interesantes de la matemática: el cálculo infinitesimal. Los griegos eran reacios a tratar con el infinito. Aristóteles creía que se podía tender al infinito al contar 1, 2, 3…etc. Pero no consideraba que podía existir un infinito actual, es decir un infinito dado todo de una vez. El “libro de arena” de Borges es, en realidad un infinito actual, y, de hecho, esta idea florece en la matemática actual, que considera el infinito como el paraíso de los matemáticos. A pesar de las reticencias griegas al infinito, Eudoxo y Arquímedes desarrollaron una especie de cálculo infinitesimal: el cálculo de exhaución.
Leibniz (uno de los creadores, junto con Newton del cálculo infinitesimal) afirmaba que un círculo era un polígono de infinitos lados. En el límite, una circunferencia de radio infinito nos parecería una recta. Esto puede parecer paradójico. Pero considérese por ejemplo, la Tierra. Cuando estamos sobre la Tierra no nos damos cuenta que es esférica, y sólo cuando nos alejamos (como los astronautas) podemos ver que es esférica. Esto se debe al gran tamaño de la Tierra. Pues, si tuviéramos una circunferencia infinita, no podríamos percibir su curvatura. En estos aspectos del cálculo, se echa mano de Arquímedes, pero “deconstruyendo” un tanto sus ideas. Se utiliza el método de exhaución de Eudoxo y Arquímedes para fundamentar el cálculo diferencial e integral. Como dice Bourbaki: “el nombre de Arquímedes no es casi siempre otra cosa que un reclamo para vender una mercancía, sin duda de gran valor, pero de la que el propio Arquímedes no se hubiera hecho responsable. Y esto sucede mucho más todavía con la diferenciación. Si una curva, cuando se trata de su rectificación, se asimila a un polígono de infinitos lados, aquí un arco ‘infinitamente pequeño’ de curva es asimilado a un segmento ‘infinitamente pequeño’ de recta”.
En el cuento de Borges “Abenjacán el bojarí muerto en su laberinto”, aparece un laberinto circular, pero tan inmenso que su borde parece recto. Borges cita aquí a Nicolás de Cusa. Nicolás de Cusa consideraba que en una circunferencia infinita el arco (curvo) entre dos puntos coincidiría con la cuerda (recta) entre esos dos mismos puntos. Todo esto fue un antecedente del cálculo infinitesimal.
El cálculo infinitesimal consiste en la diferenciación y la integración. La integración proviene de una serie de problemas que ya eran familiares a los antiguos griegos. La cuadratura del círculo es uno de los problemas que fascinaron a los matemáticos de la antigüedad y que les siguieron fascinando a lo largo de 2.000 años. Se trata de hallar, con regla y compás, un cuadrado que tendría la misma superficie que un círculo dado. Este cuadrado estaría entre el cuadrado inscrito y el cuadrado circunscrito. Pero esto es imposible. Este resultado se debe a que Pi, el número que relaciona el radio del círculo con la longitud de la circunferencia es un número trascendente, es decir un irracional que no es el resultado de ninguna raíz. El interés que tiene la cuadratura del círculo es que el intento de cuadrar superficies curvas llevaría al cálculo integral. “Cuadrar” quiere decir reducir el área de una superficie curva a la de un superficie recta (como por ejemplo uno o varios rectángulos). Una vez que se reduce a una figura recta, la superficie del círculo puede reducirse a un cuadrado.
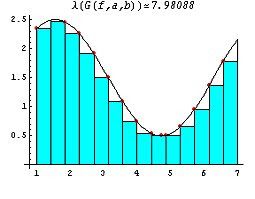
Hemos hablado de cómo los inventores del cálculo infinitesimal (Leibniz entre ellos) concibieron la circunferencia como un polígono de infinitos lados. Esto se refiere precisamente a un intento de cuadrar superficies curvas, esto es, de reducir figuras curvas a figuras rectas, cuyas medidas son más fáciles de calcular. Se trata de inscribir, primero, el cuadrado en el círculo. Más adelante, se inscribe un polígono con el doble de lados que el cuadrado, es decir, con ocho lados, todos iguales. Luego uno de dieciséis lados. Así se va aproximando el área del círculo. El resultado sólo sería exacto si el polígono tuviera infinitos lados. Naturalmente, no se puede obtener la superficie exacta. Sin embargo, se pueden obtener buenas aproximaciones. Este método está basado en el que usaron Eudoxo y Arquímedes. Hoy se conoce como cálculo integral, y es una de las partes fundamentales del análisis matemático. Hemos dicho que la integración surgió como un método de rectificación de curvas. Los griegos, desde Eudoxo, calculaban el área de una figura curva dividiéndola en figuras rectilíneas que tuvieran aproximadamente su misma área. Consideremos el dibujo del área que cae bajo una función dividido en rectángulos, con el objeto de que la suma de estos rectángulos nos dé el área que cae bajo dicha función. De ahí el símbolo de la integral inventado por Leibniz, que semeja una S. Desgraciadamente, para que la suma de los rectángulos diera exactamente el área bajo una curva el número de rectángulos habría de ser infinito. Una buena aproximación se lograría con 100 rectángulos, mejor aún, con 10.000, todavía mejor con 1.000.000 de rectángulos. Sin embargo, pese a aumentar el número de rectángulos, el resultado no se aproxima tan rápido como desearíamos. Ello se debe a que R (el conjunto de los números reales) es un continuo y los datos que maneja el computador son discretos.
El cuento de Borges nos recuerda una de las ramas más interesantes de la matemática: el cálculo infinitesimal. Los griegos eran reacios a tratar con el infinito. Aristóteles creía que se podía tender al infinito al contar 1, 2, 3…etc. Pero no consideraba que podía existir un infinito actual, es decir un infinito dado todo de una vez. El “libro de arena” de Borges es, en realidad un infinito actual, y, de hecho, esta idea florece en la matemática actual, que considera el infinito como el paraíso de los matemáticos. A pesar de las reticencias griegas al infinito, Eudoxo y Arquímedes desarrollaron una especie de cálculo infinitesimal: el cálculo de exhaución.
Leibniz (uno de los creadores, junto con Newton del cálculo infinitesimal) afirmaba que un círculo era un polígono de infinitos lados. En el límite, una circunferencia de radio infinito nos parecería una recta. Esto puede parecer paradójico. Pero considérese por ejemplo, la Tierra. Cuando estamos sobre la Tierra no nos damos cuenta que es esférica, y sólo cuando nos alejamos (como los astronautas) podemos ver que es esférica. Esto se debe al gran tamaño de la Tierra. Pues, si tuviéramos una circunferencia infinita, no podríamos percibir su curvatura. En estos aspectos del cálculo, se echa mano de Arquímedes, pero “deconstruyendo” un tanto sus ideas. Se utiliza el método de exhaución de Eudoxo y Arquímedes para fundamentar el cálculo diferencial e integral. Como dice Bourbaki: “el nombre de Arquímedes no es casi siempre otra cosa que un reclamo para vender una mercancía, sin duda de gran valor, pero de la que el propio Arquímedes no se hubiera hecho responsable. Y esto sucede mucho más todavía con la diferenciación. Si una curva, cuando se trata de su rectificación, se asimila a un polígono de infinitos lados, aquí un arco ‘infinitamente pequeño’ de curva es asimilado a un segmento ‘infinitamente pequeño’ de recta”.
En el cuento de Borges “Abenjacán el bojarí muerto en su laberinto”, aparece un laberinto circular, pero tan inmenso que su borde parece recto. Borges cita aquí a Nicolás de Cusa. Nicolás de Cusa consideraba que en una circunferencia infinita el arco (curvo) entre dos puntos coincidiría con la cuerda (recta) entre esos dos mismos puntos. Todo esto fue un antecedente del cálculo infinitesimal.
El cálculo infinitesimal consiste en la diferenciación y la integración. La integración proviene de una serie de problemas que ya eran familiares a los antiguos griegos. La cuadratura del círculo es uno de los problemas que fascinaron a los matemáticos de la antigüedad y que les siguieron fascinando a lo largo de 2.000 años. Se trata de hallar, con regla y compás, un cuadrado que tendría la misma superficie que un círculo dado. Este cuadrado estaría entre el cuadrado inscrito y el cuadrado circunscrito. Pero esto es imposible. Este resultado se debe a que Pi, el número que relaciona el radio del círculo con la longitud de la circunferencia es un número trascendente, es decir un irracional que no es el resultado de ninguna raíz. El interés que tiene la cuadratura del círculo es que el intento de cuadrar superficies curvas llevaría al cálculo integral. “Cuadrar” quiere decir reducir el área de una superficie curva a la de un superficie recta (como por ejemplo uno o varios rectángulos). Una vez que se reduce a una figura recta, la superficie del círculo puede reducirse a un cuadrado.
Hemos hablado de cómo los inventores del cálculo infinitesimal (Leibniz entre ellos) concibieron la circunferencia como un polígono de infinitos lados. Esto se refiere precisamente a un intento de cuadrar superficies curvas, esto es, de reducir figuras curvas a figuras rectas, cuyas medidas son más fáciles de calcular. Se trata de inscribir, primero, el cuadrado en el círculo. Más adelante, se inscribe un polígono con el doble de lados que el cuadrado, es decir, con ocho lados, todos iguales. Luego uno de dieciséis lados. Así se va aproximando el área del círculo. El resultado sólo sería exacto si el polígono tuviera infinitos lados. Naturalmente, no se puede obtener la superficie exacta. Sin embargo, se pueden obtener buenas aproximaciones. Este método está basado en el que usaron Eudoxo y Arquímedes. Hoy se conoce como cálculo integral, y es una de las partes fundamentales del análisis matemático. Hemos dicho que la integración surgió como un método de rectificación de curvas. Los griegos, desde Eudoxo, calculaban el área de una figura curva dividiéndola en figuras rectilíneas que tuvieran aproximadamente su misma área. Consideremos el dibujo del área que cae bajo una función dividido en rectángulos, con el objeto de que la suma de estos rectángulos nos dé el área que cae bajo dicha función. De ahí el símbolo de la integral inventado por Leibniz, que semeja una S. Desgraciadamente, para que la suma de los rectángulos diera exactamente el área bajo una curva el número de rectángulos habría de ser infinito. Una buena aproximación se lograría con 100 rectángulos, mejor aún, con 10.000, todavía mejor con 1.000.000 de rectángulos. Sin embargo, pese a aumentar el número de rectángulos, el resultado no se aproxima tan rápido como desearíamos. Ello se debe a que R (el conjunto de los números reales) es un continuo y los datos que maneja el computador son discretos.


No hay comentarios:
Publicar un comentario